CSCI716 Project: Privacy Preserving Planar Point Location

Adam Caulfield (ac7717@rit.edu)

Introduction

For the average user, many of the most serviceable applications are location-based. For instance, given your geographical coordinates, our mobile devices have applications that can help us find the closest cafe, restaurant, or gas station. Even more so, many rely on this data to be well-informed about the nearest polling location. Or in more recent years, location-based services have informed us of the closest vaccination center or concerns from contract tracing. Although these applications provide an incredibly valuable service, there is hesitancy from users to disclose personal information, such as their address or current location. Whether this is because of an untrusted third-party application providing the service or the occurrence of data breaches, fear overrules their trust in a particular service provider.

In the Computational Geometry course, we learned that Trapezoidal Maps can be used for efficient Planar Point Location. Given a set of segments, a trapezoidal map can be constructed by incrementally inserting the segments into the plane. The trapezoidal map can be abstracted as a Directed Acyclic Graph (DAG), and traversing the DAG by conducting comparisons will allow for Planar Point Location. Through this project, I want to explore the question: Can Planar Point Location be conducted in a Trapezoidal Map, given that the point coordinates are encrypted? Homomorphic Encryption (HE) is an encryption scheme allowing for arithmetic over data without decryption. Because of this, I aim to combine HE with Trapezoidal Maps to conduct Privacy-Preserving Planar Point Location.

Related Works

This section describes two works by Aloufi et al. that are significantly related and any critical similarities and differences to my project. Additional links to background resources which I used as a part of the background research phase, are linked in the Additional Resources section.

In "Universal Location Referencing and Homomorphic Evaluation of Geospatial Query" [July 2019], Aloufi et al. propose a technique to achieve geospatial queries given the geospatial data of users are encrypted. They achieve a similar goal to accomplishing queries based upon encrypted geographic data using HE. I will be approaching a different area regarding how location is represented. In this work, a user's location is defined by a series of rectangular bounding boxes, and queries answer with the coordinate of another rectangular bounding box, the size of which depends upon specific privacy settings. In this project, a user's location will be their exact integer coordinates, and the query will return the ID of the trapezoid shape in which the point is located.

In "Blindfolded Evaluation of Random Forests with Multi-Key Homomorphic Encryption" [July 2019], Aloufi et al. layout algorithms and protocols for evaluating random forests given features that are encrypted with multi-key homomorphic encryption. In my project, the system model is assumed to be an interaction between one user and a service provider. A similarity is between the evaluation of a decision tree and a DAG, which is the target structure in both their and my work. In their work, they outline an algorithm to securely compare two integers that are encrypted in HE. I use this algorithm in my project because of the requirement to conduct comparisons when traversing the DAG. In this project, evaluating some nodes (Y-Nodes) requires additional homomorphic operations besides the secure comparison alone.

Approach and Implementation

Trapezoidal Map & Planar Point Location

First, the functions are needed to construct the trapezoidal map from a set of segments. I will use the incremental construction algorithm to generate the trapezoidal map from a set of segments. A Directed Acyclic Graph (DAG) is used as a data structure to represent the trapezoidal map. Figure 1 demonstrates the incremental construction algorithm, changes to the trapezoid boundaries as segments are added to the plane, and changes to the DAG as each segment is added.

Note: For efficiency, I allowed the map in my implementation to contain "trapezoid" regions with more than four sides (aka polygon regions such as T3 and T5 in the final map below). Evaluating the comparison for a node in HE is ultimately the bottleneck, so having fewer nodes is more efficient. Therefore this is a way to reduce the number of total nodes in the DAG by avoiding multiple nodes for one segment.

In the DAG, there are three classes of nodes: X-Node (gray), Y-Node (blue), and Leaf-Node (yellow). An X-Node corresponds to an X-coordinate of one of the vertices of a segment. The left child of an X-Node represents nodes to the left of the X-vertex of that node, and the right child represents nodes to the right. The Y-Node represents a segment's slope and intercept. The left child of a Y-Node is a node below the segment, and the right child represents nodes above the segment. Finally, Leaf-Node represents a unique region in the map. Leaf nodes do not have any child nodes.

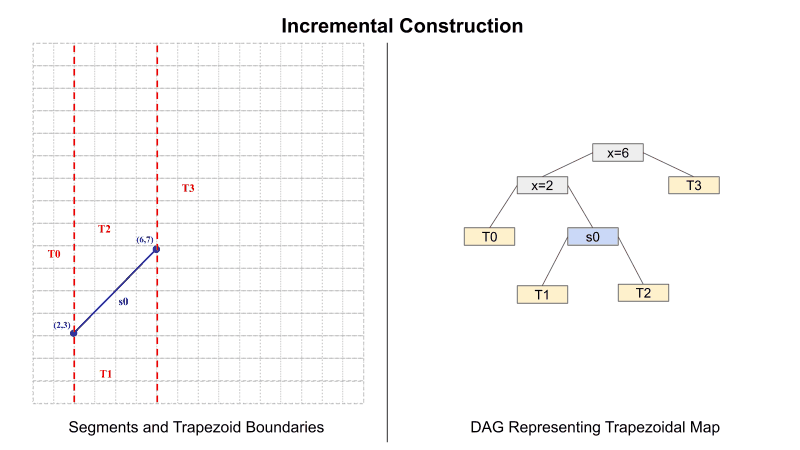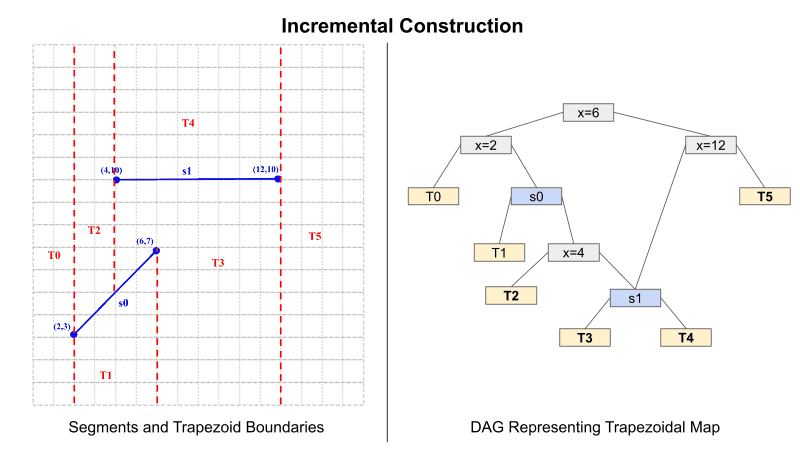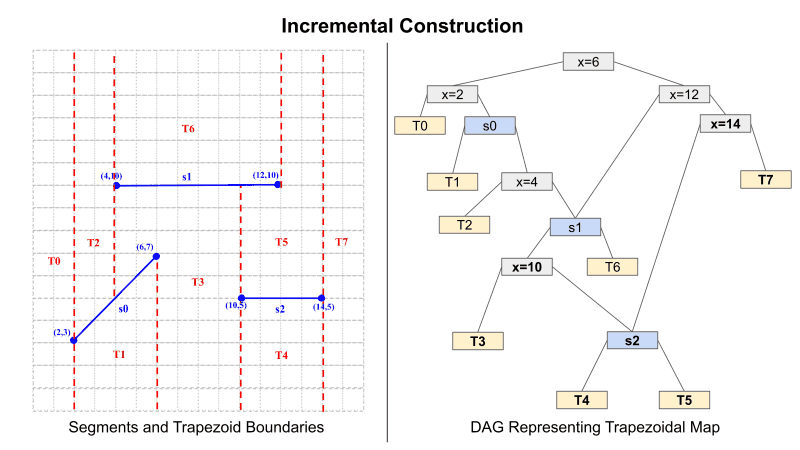
Incremental Construction

Figure 1: Incremental Construction of Trapezoidal Map

Inserting a segment into the DAG requires creating three nodes. First, two X-Nodes for the left and right vertices of the segment. The third is one Y-Node representing the slope and intercept of the segment. Nodes are added by following the comparison rules for each node type. For an X-Node, the comparison is between the X-values. If less than or equal to, traverse left. If greater than, traverse right. The case is the same with Y-nodes but comparing Y-values instead.

Planar point location follows a similar pattern to inserting a new segment. Figure 2 demonstrates how to traverse the DAG to find the trapezoid which holds the point (8,7). When reaching an X-Node, the X-coordinate of the point is compared to the X-value that the node represents. Once again, if less than or equal to, traverse left. Otherwise, traverse right. When reaching a Y-Node, it must be determined whether the point is above or below the segment. This is done by determining the Y-value on the segment for the points X coordinate. Then once this is determined, compare the actual Y coordinate to the on-segment value. Once again, if less than or equal to, traverse left. Otherwise, traverse right. This process is repeated until a leaf node is reached, and once this has occurred, the leaf node represents the region that contains the point.

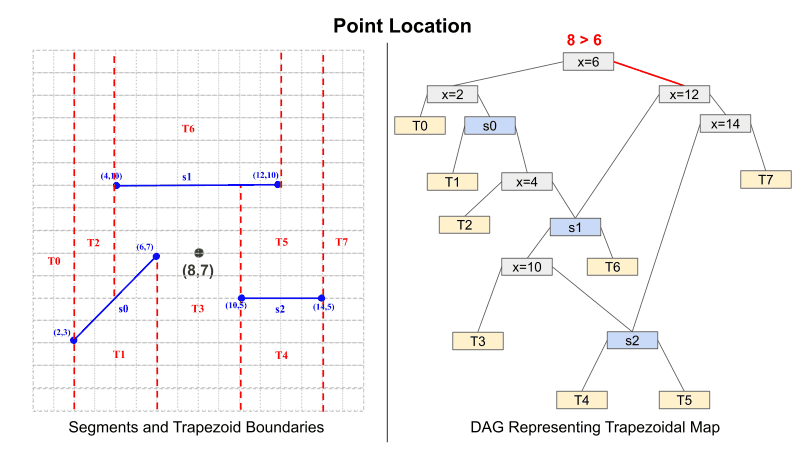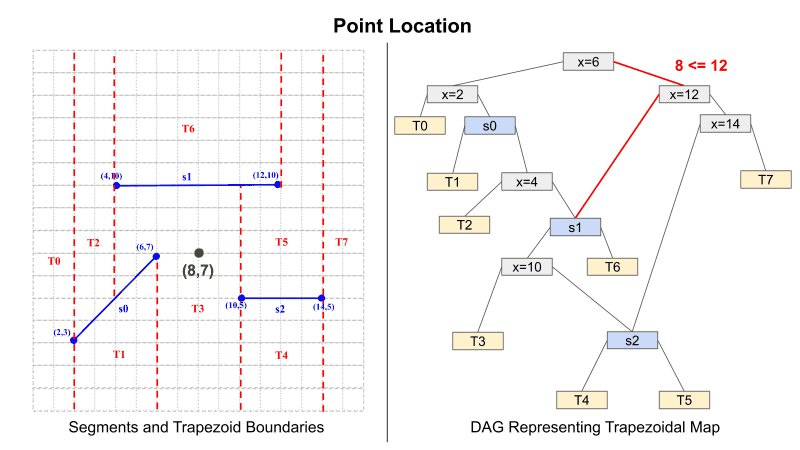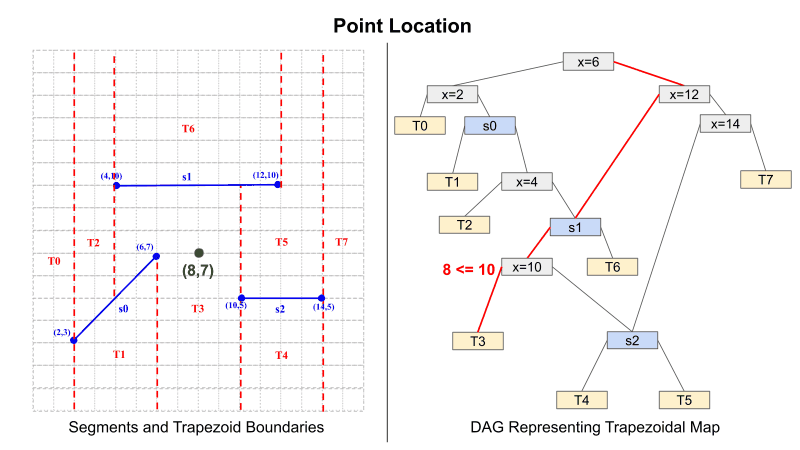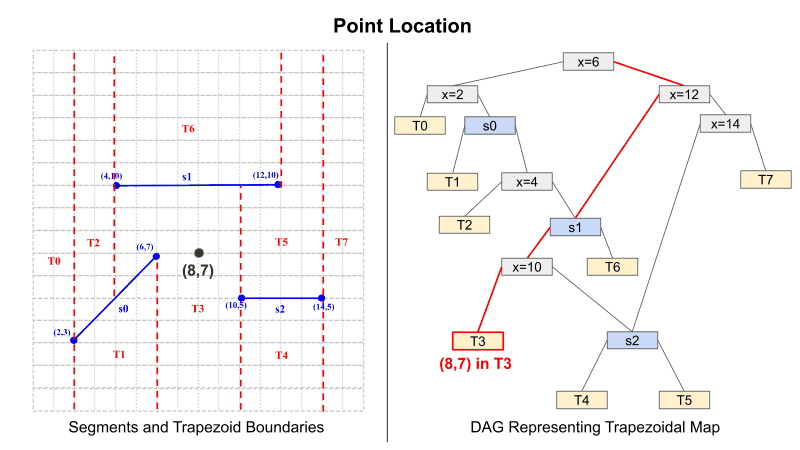
Point Location

Figure 2: Planar Point Location using Trapezoidal Map

Evaluating Homomorphically

Homomorphic encryption (HE), is an encryption scheme that allows for addition and multiplication without requiring decryption. This allows for operations to occur on private data without revealing its privacy. Given a point that is encrypted using HE, locating the point using planar point location via a trapezoidal map is reduced to the ability to evaluate the X-Nodes and Y-Nodes in the DAG homomorphically. I use the C++ library HElib for implementation.

An approach that I apply to this work comes from Aloufi et al. , in which they propose a homomorphic comparison function of two integers that are represented as a vector of their binary format. Ex: 5 → [1, 0, 1, 0]. This is possible using schemes such as BGV, which I use in this project. This can be used to evaluate X-Nodes and as a step in evaluating the Y-Node. However, given that the integers will be converted to vectors of their binary and then encrypted in that form, additional functions are required to evaluate the Y-Node.

Because of the encoded format required for the secure comparison, I develop functions that operate on HE ciphertexts and complete binary addition and multiplication, which will be required to evaluate a Y-Node. My approach is to implement the equivalent of their logic gates forms. In HE, we are limited to addition and multiplication. Figure 3 demonstrates how core logic gates, XOR, AND, and OR, can be translated into arithmetic using only + and * operators given two bits A and B.

A B XOR(A,B) AND(A,B) OR(A,B)
0 0 0 0 0
0 1 1 0 1
1 0 1 0 1
1 1 0 1 1
Arithmetic form A + B A * B A + B + A*B

Figure 3: Truth Tables and Arithmetic form for Logic Gates

Using these logic gates are core building blocks, I have implemented functions that perform binary addition and binary multiplication. Because these two components at their core use XOR, OR, and AND operators, I can represent them using the arithmetic in Figure 3. Similarly, shift operators are required and are possible in HElib. Evaluating a Y-Node follows this procedure: given a point (px, py) as ciphertext and the Y-Node specified by the segment with slope-intercept of (dy/dx, b) in plaintext, compare py to dy/dx * px + b. Conducting division is unideal in the HE domain, so I have translated this into an equal comparison between dx*py and dy*px + dx*b. (Simply multiplying the same inequality by dx). This achieves the same comparison without division. This requires two binary multiplications of ciphertext 1) dx*py and 2) dy*px and one addition dy*px + dx*b. The product dx*b does not require binary multiplication because both of these components are in plaintext, and thus it is more efficient to multiply using integer multiplication than encoding the result into its binary form.

.

Given an X- and Y-Node can be evaluated homomorphically, the final result is produced by the following. Because we have no knowledge of the point's coordinates, all paths in the DAG must be evaluated. Each path accumulates a result by taking the AND of each intermediate result. For example, in Figure 2 the path result is found by T3 = (px > 6) AND (px <= 12) AND (py <= s1(px)) AND (px <= 10). All Path results (like T3) will store a vector with either all 1's given that it is True or all 0's given that it is False. Because of this, the final result is computed by accumulating the result only in the index of the trapezoid ID. For instance: T_final = {1, 0, 0, ... } * T0 + {0, 1, 0, ...} * T1 + ... and so on. This will return a ciphertext that encrypts a vector; that vector is a sparse vector that has a value of 1 only at the index, which is the ID of the trapezoid the point is located in.

Parallelization

A default approach is to traverse the DAG using recursion and accumulating the result. The problem with this (serial) approach is that evaluating one node is quite slow due to the shifts and multiplications required. Because of this, I implemented two phases of parallelization. First, each node will be evaluated on its own, and the result of that node will be stored. This is because the evaluation result of a single node does not depend on another (for instance, because of encryption, the comparison result for x<=6 has no effect on the comparison x<=12. Both must be evaluated, and one does not use the result of the other in its comparison). For this reason, node evaluation is done in parallel. After this, all that is required is accumulating the results by 1) Getting the path result by AND-ing (multiply) node results on the path and 2) filtering and summing the results. Because of this, I choose to parallelize the step for getting the path results since they can be determined independently. Once each path result is determined, the filtering and summing step is completed in parallel.

System Overview

Figure 4 shows an overview of the interaction between the User and the Service Provider.

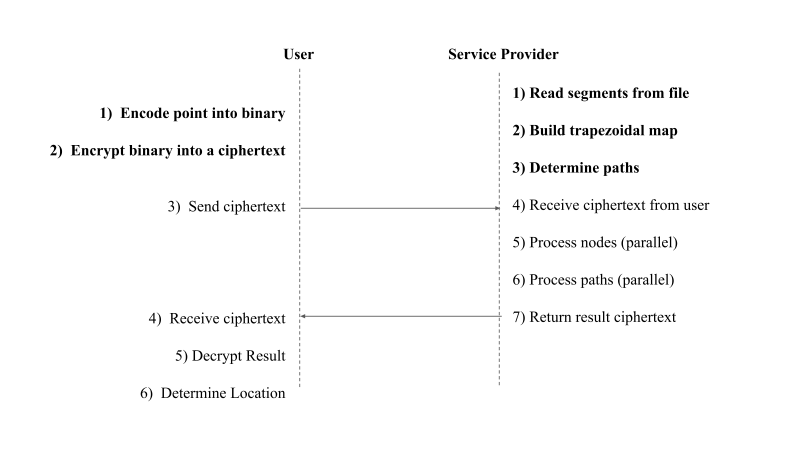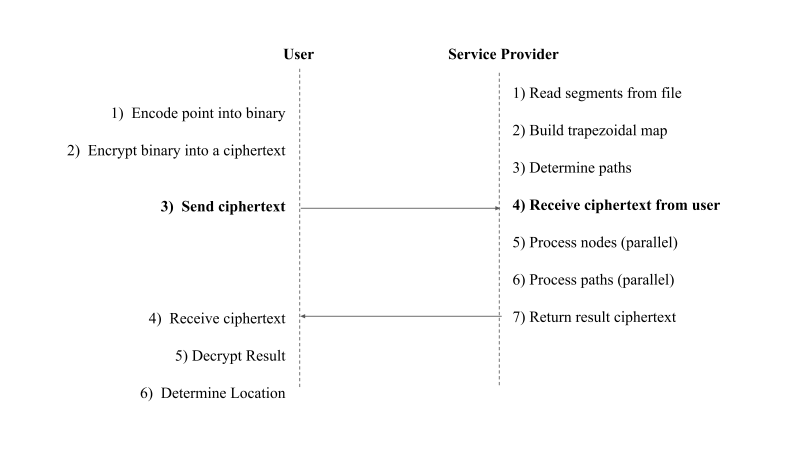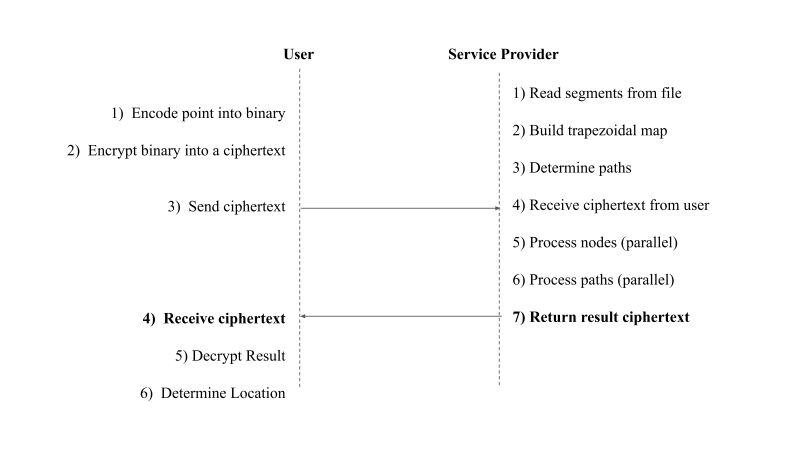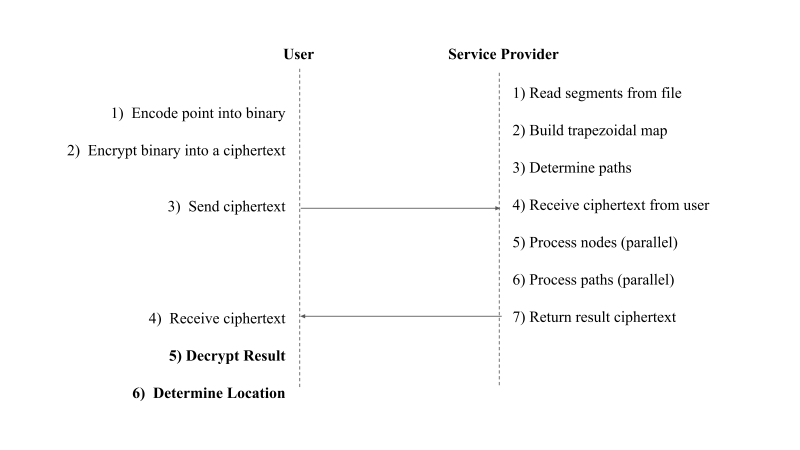
System overview

Figure 4: Overview of system between Client and Service Provider

Source Code, Documentation, and Demo

The project code base and instructions to run the program are located at my Github Page

To view the classes and application structure visit the Documentation

To view a presentation and 10-minute demo on this information visit this Google Drive link

Project Timeline

Week 4-5 - Conduct background research

Week 5-8 - Write building block functions

Week 8-10 - Implement core homomorphic functions

Week 11-13 - Implement tree structure

Week 13-14 - Test with variable region vertices and debug

Week 15 - Prepare and give final presentation

Additional Resources